Солитонная модель Материи

• Изъяны абстрактно-формальной парадигмы познания
• Парадокс в теоретической физике
•   Обоснование наличия Предматерии
•   Солитонная модель Материи
•     «Фотоны» и «нейтрино» – одиночные волны-импульсы
•     Сущность «массы» и «тяготения»
•     Сущность «заряда», «электрополя» и электромагнетизма»
•     Сущность «кварков» и барионов
• Сущностная космология
• Сопоставление сущностных и абстрактных единиц измерения
•   Научная значимость открытия
•   Практическая значимость открытия
• Методика верификации модели
• Список литературы

Научным фактом является возникновение и распространение в физической системе «твердое тело» волновых процессов различных типов, в том числе поперечных и продольных бегущих волн. Различие между ними состоит как в способе возбуждения волны, так и в направлении смещения (возбуждения) элементов при распространении волны.

При распространении поперечных волн смещение (возбуждение) элементов происходит в направлении, перпендикулярном распространению волны, а при распространении продольных волн смещение (возбуждение) элементов происходит в направлении распространения волны. Причиной возникновения поперечной волны является деформация сдвига одного слоя (элемента) среды относительно другого, а причиной возникновения продольной волны - деформация сжатия/растяжения.

Сначала рассмотрим поперечные волны - фотоны. Поскольку в направлении, перпендикулярном фронту волны, смещение (возбуждение) элементов Предматерии происходят поочерёдно в двух измерениях, то результирующее движение конца вектора скорости смещения (возбуждения) от внешнего воздействия элементов Предматерии, участвующих в колебательном процессе, будет винтовым. Такую форму движения создаёт поступательное движение фронта волны и циркулярно поляризованное смещение (возбуждение) элементов Предматерии, обусловленное структурной организацией Предматерии.

Именно свойство поперечных волн и способ их возбуждения позволило детализировать структурную организацию элементов в Предматерии в виде послойных винтовых плоскостей, создающих циркулярно поляризованное смещение (возбуждение) элементов Предматерии.

Таким образом, фотон-импульс представляет собой сложную физическую систему, в которой совместились свойства классического гармонического осциллятора (система, совершающая свободные колебания около положения устойчивого равновесия по закону синуса или косинуса) и ротатора (система, у которой частицы вращаются вокруг общей оси, двигающейся поступательно). При этом параметры и осциллятора, и ротатора, и поступательного движения определяются упругими и инерционными свойствами среды – элементов Предматерии – и характеристиками внешнего воздействия.

Помимо энергии (заключенной в колеблющихся элементах Предматерии и передающейся по направлению фронта волны), фотон-импульс характеризуется еще двумя физическими величинами, очень важными для определения его взаимодействия с окружающей средой: это момент количества движения - спин (от сложного пространственного смещения элементов, как бы поочередно участвующих во вращательном движении) и импульс (от поступательного движения энергии).

Фотон, как бегущая волна, не может иметь «массы покоя» и образовывать гравитационное поле – разъяснение этому приведено в разделе о «массе» и «тяготении».

Наибольший интерес представляет определение связи параметров фотона (энергии, спина и импульса) с параметрами элементов Предматерии (плотностью, жесткостью, добротностью и геометрическими размерами).

Рассмотрим процессы образования фотонов в пространстве Предматерии.

При отклонении произвольным внешним воздействием элемента Предматерии от положения равновесия (или покоя) он начинает совершать сложные колебательные движения с частотой, являющейся результирующей между собственной частотой (частота свободных колебаний, зависящая только от жесткости упругих связей и плотности элемента Предматерии) и частотой внешнего воздействия, а амплитуда колебаний зависит от величины переданной элементу энергии. Для иллюстрации сущности процесса приведем уравнения для описания одномерных вынужденных колебаний – это значительно упростит выкладки, а переход к описанию реальной системы с тремя степенями свободы сложностей не представляет.

Дифференциальное уравнение движения при вынужденном возбуждении (в предположении отсутствия сил сопротивления среды) имеет вид:

ÿ + ω₀² ý = F₀ sin(θt + β)/m₀, (1)

где y – обобщенная координата, её первая (ý) и вторая (ÿ) производные;

ω₀ – круговая частота собственных колебаний;

F₀ – обобщенная сила;

θ – круговая частота обобщенной силы;

β – начальная фаза обобщенной силы;

m₀ – масса единичного элемента, к которому приложена внешняя сила.

Решением представленного линейного неоднородного уравнения будет сумма решений однородного уравнения и частного решения неоднородного уравнения (для фотона рассматриваем случай отсутствия резонанса, то есть ω≠θ):

y = Asin(ωt + α) + F₀ sin(θt + β) / m₀(ω² – θ²), (2)

где A и α – постоянные, определяемые из начальных условий.

Как видно из формулы 2, результирующее движение единичного элемента состоит из двух гармонических колебаний с частотами ω и θ.

В пространстве трех измерений для описания фотона можно применить неоднородное волновое уравнение:

□W = f (x,y,z,t), (3)

где □ – оператор Д"Аламбера;

W – функция, характеризующая возмущение среды в точке с координатами x,y,z в момент времени t;

f (x,y,z,t) – внешнее возмущение в функции координат и времени.

Траектория огибающей результирующего движения элементов имеет вид винтовой линии с шагом винта, равным длине волны возмущающего воздействия, а сам "винт" является синусоидой с частотой θ, модулированная частотой ω (Рис.3).

Рис. 3. Изображение процесса модулирования волны-возмущения резонансной волной
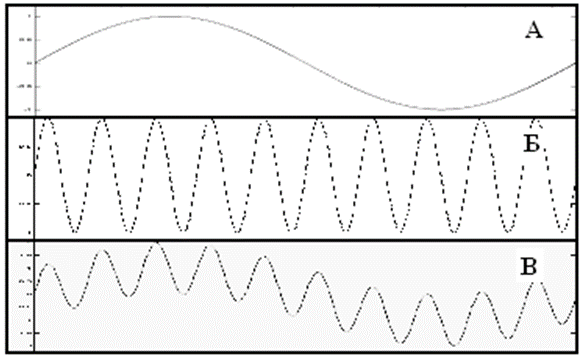
А - график волнения возмущения; Б - график волны-резонанса; В - график результирующего волнового процесса.

Кинетическая энергия фотона (гармонического осциллятора – ротатора) является квадратичной формой скоростей обобщенных координат:

E_k = m₀ v_ω v_θ/2 = m₀ (ω₀A₀)(θ A_θ) /2, (4)

где m₀ – масса элементов Предматерии, участвующих в колебательном процессе;

ω₀ – круговая частота собственных колебаний;

A₀ – амплитуда колебаний с частотой собственных колебаний;

θ - круговая частота колебаний внешнего воздействия;

A_θ - амплитуда колебаний с частотой колебаний внешнего воздействия.

Поскольку v_ω= ω₀A₀ = c,

где c – скорость фотона в элементах Предматерии, то есть, скорость света,

то E_k = h θ /2π = m₀ c θ A_θ /2, (5)

h = 2π m₀ c A_θ /2 = π m₀ c A_θ (6)

Момент количества движения (спин) фотона как ротатора можно определить по формуле:

L = m_r ω_rR_r² (7)

Одновременно известно, что спин фотона также равен:

L = h / 2 π, (8)

где h – постоянная Планка.

Через постоянную Планка можно выразить и энергию фотона:

E = hf₀, (9)

где f₀ – частота фотона.

Сопоставляя формулу 9 с формулами 1 и 2, получим:

E₀ = m₀ ω₀² A₀² /2 = m₀ 4 π² f₀² A₀² /2 = h f₀ (10)

E_r = m_r ω_r² R_r² /2 = m_r 4 π² f_r² R_r² /2 = h f_r (11)

откуда:

h = m₀ 2 π² f₀A₀² (12)

h = m_r 2 π² f_rR_r² (13)

Из формул 12 и 13 можно сделать вывод о том, что сущность постоянной Планка есть такое минимальное действие внешней силы (для колебательного процесса) или такой минимальный вращающий момент (для вращательного процесса), которые могут запустить устойчивый колебательный или вращательный процесс в элементах Предматерии.

Наличие у поперечных волн (фотонов) "спина" обеспечивает структурная организация элементов Предматерии – двухслойная гексагональная плотно упакованная система расположения элементов с одинаковыми ребрами и углами и с координационным числом, равным 12, то есть, каждый элемент в пространстве трех измерений связан одновременно с 12 другими элементами (Рис. 1 и 2) – при которой возбуждение колебаний продольных и поперечных волн в элементах Предматерии происходит по траектории винтовой линии. Другие формы упаковки не позволяют реализовать наличия у продольных и поперечных волн "спина", то есть винтовой формы траектории бегущих волн.

Элементы Предматерии не могут идеально, без потерь, проводить колебания, поэтому должно существовать волновое сопротивление Предматерии, которое приводит к потере энергии бегущих волн, что проявляется снижением частоты их колебаний. Поскольку потери энергии в элементах Предматерии (как в осцилляторах с высокой добротностью) весьма незначительное, то снижение частоты колебаний фотонов обнаруживается только на космологических расстояниях – именно так можно объяснить наблюдаемый эффект "космологического красного смещения". И чем дальше находится объект, испускающий фотоны, тем больший путь они проходят, и тем больше снижается их частота.

Следует отметить, что волновое сопротивление элементов Предматерии, как декремент затухания, давно установлено – это, по нашему мнению, так называемая "постоянная Хаббла" (Н), неверно трактуемая как "коэффициент пропорциональности между скоростью удаления внегалактических объектов, вызванного космологическим расширением видимой Вселенной, и расстоянием до них".

если γ = H = 2,310⁻¹⁸ с⁻¹ (14)

где γ – декремент затухания,

Н - постоянная Хаббла,

то время затухания (т.е. уменьшение амплитуды в 2,71828 (е) раз:

τ_зат = 1/γ = 4,354 ± 0,012)10¹⁷ с или (13,798 ± 0,037)10⁹ лет (15)

Это время учёными трактуется как срок до Большого Взрыва, но, по нашему мнению, такая модель рождения Вселенной является ошибочной, поскольку:

- приводит к необоснованному выводу о Вселенной, якобы изначально собранной в точечный объект, в котором сосредоточена некая первичная бесструктурная субстанция, из которой при взрыве возникают частицы и поля;

- не может объяснить, как в этой точечной бесструктурной субстанции сохранены, а затем и воспроизводятся алгоритмы порождения частиц и полей, а также большой набор их параметров – формы, размера, массы, заряда, спина и т.д.

Космологическая модель Вселенной, построенная исключительно на известных научных фактах и не включающая ненаучных предположений, приведена в разделе "Научная космологическая модель Вселенной".

Рассмотрим существование продольных волн в упругой среде из элементов Предматерии. Известно, что продольные волны могут существовать в среде с любым агрегатным состоянием – тем более, в упругой среде. В предлагаемой модели в качестве продольных волн в виде одиночных структурно устойчивых импульсов выступают нейтрино. Демонстрация процесса образования нейтрино как продольной волны приведено в разделе о распаде нейтрона.

В связи с тем, что структура Предматерии обеспечивает движение одиночных волн-импульсов по траектории винтовой линии, то нейтрино, помимо характеристики прямолинейного движения (импульс), имеют и вращательную характеристику движения (спин). Условно принято, что продольные волны-импульсы с левой спиральностью именуются "нейтрино", а с правой спиральностью – "антинейтрино".

Различие между нейтрино различных видов (электронное, мюонное и таонное) определяется тремя параметрами:

1. количеством вовлеченных в продольную волну-импульс элементов Предматерии (сечение продольной волны);
2. частотой бегущей волны;
3. энергией бегущей волны.

Располагая моделью нейтрино и зная сечение взаимодействия нейтрино (составляет примерно 9,3 ^. 10^-48 м²), можно определить "диаметр" нейтрино:

d = (4 x S / π ) ^0,5 = (4 x 9,3 ^. 10^-48 м² / π ) ^0,5 = 3,4 x 10^-24 м. (16)

Как всякая упругая среда, элементы Предматерии характеризуются модулями упругости:

E – модуль продольной упругости, или модуль Юнга, Н/м²;

G - модуль поперечной упругости, Н/м².

От величины указанных модулей зависят скорости распространения упругих волн в элементах Предматерии:

продольных c_l= (E/ρ)^0,5 (17)

и поперечных c_t = (G/ρ)^0,5 (18)

где ρ – плотность элементов Предматерии, кг/м³.

Для всех известных науке материалов между E и G существует зависимость:

G = E/2(1+ν), (19)

где ν – коэффициент Пуассона - параметр, изменяющийся для различных "земных" материалов в пределах от 0 до 0,5 – чаще около 0,3.

Если подставить в соотношение 19 значения параметра ν, а затем по формулам 17 и 18 вычислить соотношение между скоростями продольных и поперечных волн, то получим:

при ν = 0 c_l = 1,414c_t; (20)

при ν = 0,3 c_l = 1,612c_t; (21)

при ν = 0,5 c_l = 1,732c_t. (22)

Таким образом, в предположении, что в Предматерии возможны аналогичные соотношения между модулями продольной и поперечной упругости, получаем, что скорость продольных волн может быть больше скорости поперечных волн примерно в 1,4 – 1,7 раза.

В научных публикациях имеются сведения о том, что измеренные скорости распространения нейтрино примерно равны скорости света, то есть, скорости поперечных волн. Пока что эти сведения не вполне достоверны, но в случае их подтверждения, можно утверждать, что Предматерия является ауксетиком - материалом, имеющим отрицательное значение коэффициента Пуассона.

То есть, при равенстве скоростей нейтрино и фотонов (как продольных и поперечных волн-импульсов) коэффициент Пуассона ν = - 0,5 и модуль продольной упругости "E" равен модулю поперечной упругости "G".

Материалы с таким соотношением модулей упругости при сжатии (возбуждении) не увеличивают, а уменьшают свои размеры, то есть элементы Предматерии при сжатии (возбуждении) не увеличиваются в размерах, а наоборот – уменьшаются, а это может послужить доказательством наличия сложной внутренней структуры элементов Предматерии.

Таким образом, точное установление скорости нейтрино позволит достоверно определить и свойство самих элементов Предматерии, и свойство связей между элементами, при которых создаются условия для равенства модулей продольной и поперечной упругости, то есть, для одинаковости восприятия элементами Предматерии усилий сжатия и сдвига.

В настоящее время изученность нейтрино недостаточна для суждения о том, каковы параметры каждого из существующих видов нейтрино (электронного, мюонного, таонного), однако некоторые предположения высказать всё же возможно:

Во-первых, частота бегущей волны у таонного нейтрино, возможно, больше, чем у мюонного, а у мюонного больше, чем у электронного, поскольку в таких же соотношениях находятся энергии таона, мюона и электрона. Потому что "рождение" нейтрино различных видов связано с участием соответствующих частиц.

Во-вторых, нейтрино различных видов могут "преобразовываться" друг в друга ("осцилляция нейтрино") при потере или прибавлении энергии - при этом может изменяться сечение продольной волны или её частота.

В-третьих, нейтрино, как бегущие волны, не могут иметь "массы покоя" и, как следствие, не могут образовывать в пространстве Предматерии "гравитационное поле", как будет показано в разделе о "массе" и "тяготении".